Answer:
(-7, 9)
Explanation:
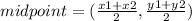
(x₁, y₁) is the coordinates of one endpoint
(x₂, y₂) is the coordinates of the other endpoint
Given that the midpoint V has coordinates of (-1, 3),
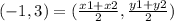
Substitute the coordinates of G:
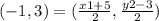
By observation:
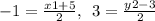
-1(2)= x₁ +5 (×2 on both sides)
-2= x₁ +5
x₁= -2 -5
x₁= -7
3(2)= y₂ -3 (×2 on both sides)
6= y₂ -3
y₂= 6 +3
y₂= 9
Thus, the coordinates of H is (-7, 9).