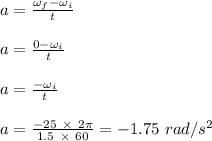Question

A 1.15 kg grinding wheel 20 cm in diameter is spinning clockwise at rate of 25 revolutions per second. When the power to the grinder is turned off, the grinding wheel slows with constant angular acceleration and takes 1.5 minutes to come to rest.

What was the linear acceleration (in m / sec²) of grinding wheel as it comes to rest if we take a clockwise rotation as positive?


Answer 1

Choose...

How many revolution did the wheel make during the time it was coming to rest?


Answer 2

Choose...

What was the angular acceleration (in rad / sec²) of grinding wheel as it comes to rest if we take a counterclockwise rotation as positive?

Answer 1

(a) Linear acceleration of the wheel is 0.175 m/s²

(b) The angular acceleration is -1.75 rad/s²

Step-by-step explanation:

Given;

mass of the grinding wheel, m = 1.15 kg

diameter of the grinding wheel, d = 20 cm

radius of wheel, r = 10 cm = 0.1 m

angular speed of the wheel, ω = 25 revolutions per second

time for the wheel to come to rest, t = 1.5 minutes

The linear speed is calculated as;

v = ωr

`v = (25 \ rev)/(s) \ * \ (2\pi \ rad)/(1 \ rev) \ * \ 0.1 \ m\\\\v = 15.71 \ m/s`

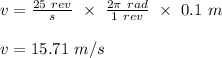
(a) Linear acceleration of the wheel is calculated;

`a = (v)/(t) \\\\a = (15.71)/(1.5 \ * \ 60) \\\\a= 0.175 \ m/s^2`

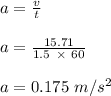
(b) The angular acceleration is calculated as;

`a = (\omega_f - \omega_i )/(t) \\\\a = (0-\omega_i)/(t) \\\\a = (-\omega_i)/(t) \\\\a = (- 25 \ * \ 2\pi)/(1.5 \ * \ 60) = -1.75 \ rad/s^2`