Question

Consider the two functions. Which statement is true?

A) Function 1 has the greater y-intercept by 1 unit
B) Function 2 has the greater y-intercept by 1 unit
C) Function 1 has the greater y-intercept by 1 2 unit
D) Function 2 has the greater y-intercept by 1 2 unit

Function 2
x y
2 11
3 14
4 17
5 20

Answer 1

function 2 has the greater y intercept by 1 unit

Explanation:

Function 2

x y

2 11

3 14

4 17

5 20

Lets frame equation for function 2 and then we find y intercept

Slope = change in y / change in x

slop
`m = (14-11)/(3-2) = 3`

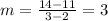
we use equation y = mx + b

where m is the slope and b is the y intercept

We got m = 3, to find b we plug in x=2 and y =11 in y=mx+b

11= 3(2) + b

11= 6 + b

Subtract 6 on both sides

b= 5

So y intercept of function 2 is 5

Now we find the y intercept of function 1 from the given graph

y intercept is the point where the graph crosses y axis

the graph of function 2 crosses y axis at 4

So y intercept of function 1 is 4

Hence function 2 has the greater y intercept by 1 unit

Answer 2

Option B. Function
`2` has the greater y-intercept by
`1` unit

Explanation:

we know that

The y-intercept is the value of y when the value of x is equal to zero

In this problem

The y-intercept of the function
`1` is
`4` ----> observing the graph

Step 1

Find the slope of the function
`2`

The formula to calculate the slope between two points is equal to

`m=(y2-y1)/(x2-x1)`

we have

`A(2,11)\ B(3,14)`

substitute

`m=(14-11)/(3-2)=3`

Step 2

Find the equation of the function
`2`

The equation of the line into slope intercept form is equal to

`y=mx+b`

we have

`m=3`

`A(2,11)`

substitute

`11=3(2)+b`

`b=5` ------> the y-intercept of the function
`2`

therefore

Function
`2` has the greater y-intercept by
`1` unit