Answer:
6.25% of chances.
Explanation:
Here we can use a standard probability definition, which says that the probability of happening an event is the fraction between total possible cases and total events:
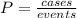
In this case, the cases are spades, and total events are spades, clubs, hearts and diamonds, which sum 52. Replacing all values:
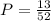
However, in this problem, after we take out a card, we will place it back again. And the probability we have to calculate is the chance of getting spades twice in a row. To do that, we have to consider that each card is an independent success, which means that neither one affects on the outcome of another one, and this is expressed as a multiplication.
So, for each time we are gonna take a spade card, the probability is 13/52, doing it twice, we have:

Therefore, there is a 6.25% of chances that we will pull out two spade cards in a row.