Answer:
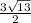
Explanation:
First we have to identify the parallel sides of the trapezium.
We know that the slopes are equal for parallel lines.
Slope of (x₁,y₁) and (x₂,y₂) is given by
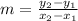
Slope of AB:
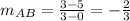
Slope of BC:
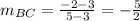
Slope of CD:
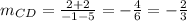
Slope of DA:
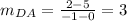
We see that the slopes of AB and CD are equal, so, AB and CD are the parallel sides.
The length of the midsegment = (1/2)*(length of base1 + length of base2 )
Length of the bases can be calculated using distance formula,
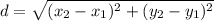
AB =
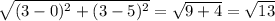
CD =

Length of the midsegment = (1/2) (√13 + 2√13) =3√13/2