1 Answer

Thet · Answer 1 · 2019-11-12T23:56:03+0000

Answer:

There are 40 girls and 24 boys in the camp

Explanation:

let
be the number of boys and
be the number of girls in the camp, then when know that

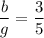(b)/(g) = (3)/(5) (this says that the ratio of boys to girls is 3: 5)

And since there are a total of 64 campers, we have

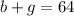b+g =64 (this says that the total number of boys an girls must 64)

Thus, we have two equations and two unknowns:

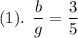
$(1). \: \: (b)/(g) = (3)/(5)$

$(2). \: \:b+g =64$

and we solve this system by first solving for
in equation (1):

b= (3)/(5)g,

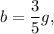
and substituting it into equation (2):

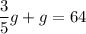
(3)/(5)g+g=64

solving for
we get:

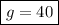$\boxed{g=40}$ .

Putting
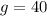g=40 into equation (2), we solve for
to get:

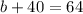
b+40=64

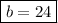
$\boxed{b=24}$

Thus, there are 40 girls and 24 boys in the camp.

Please log in or register to add a comment.