Question

Find the length of AC. Round answer to the nearest tenth.

Answer 1

Answer: The required length of AC is 16.1 units.

Step-by-step explanation: We are given to find the length of side AC of triangle ABC.

From the figure, we note that

the triangle ABC is a right-angled triangle, where

m∠C = 90°, m∠A = 32° and BC = 10 units.

For the acute angle A, side AC is the base and side BC is the perpendicular.

So, from trigonometric ratios, we have

`\tan m\angle A=(perpendicular)/(base)\\\\\\\Rightarrow \tan32^\circ=(BC)/(AC)\\\\\\\Rightarrow \tan32^\circ=(10)/(AC)\\\\\\\Rightarrow 0.62=(10)/(AC)\\\\\\\Rightarrow AC=(10)/(0.62)\\\\\Rightarrow AC=16.13.`

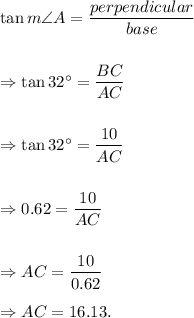
Rounding to nearest tenth, we get

AC = 16.1 units.

Thus, the required length of AC is 16.1 units.

Answer 2

16.0

Explanation:

The mnemonic SOH CAH TOA reminds you ...

... Tan = Opposite/Adjacent

... tan(32°) = 10/AC

Multiplying by AC and dividing by the tangent gives you ...

... 10/tan(32°) = AC = 16.0