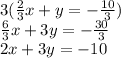Question

Write the standard form of the line that is parallel to 2 x + 3 y = 4 and passes through the point (1, -4). Include your work in your final answer. Type your answer in the box provided or use the upload option to submit your solution.

Answer 1

`2x+3y=-10`

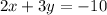
Explanation:

We can write the equation of a line in 3 different forms including slope intercept, point-slope, and standard depending on the information we have. We have a point given and a slope we can find from the standard equation. We will chose point-slope since we have a point and can find the slope. We can then convert into standard.

Point slope:
`y-y_1=m(x-x_1)`

We must find the slope by converting the standard form into slop-intercept.

`2x+3y=4\\2x-2x+3y=4-2x\\3y=4-2x\\(3y)/(3) =(4-2x)/(3)`

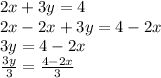
We rearrange in y=mx+b form to
`y=-(2)/(3)x+(4)/(3)`.

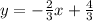Since parallel lines have the same slope
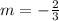`m=-(2)/(3)` is the slope for our line. We will now use point slope form.

We will substitute
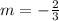`m=-(2)/(3)` and
`x_1=1\\y_1=-4`.

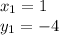`[tex]y+4=-(2)/(3)x+(2)/(3) \\y+4-4=-(2)/(3)x+(2)/(3)-4\\y=-(2)/(3)x+(2)/(3)-4\\y=-(2)/(3)x+(2)/(3)-(12)/(3) \\(2)/(3)x+y=-(2)/(3)x+-(2)/(3)x-(10)/(3)`[/tex]

This simplifies to
`(2)/(3)x+y=-(10)/(3)`.

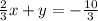To be in standard form, the coefficients of x and y must not be 0 or any fractions. The coefficient of x muxt be positive. To meet these requirements, we multiply the entire equation by 3.

`3((2)/(3)x+y=-(10)/(3))\\(6)/(3)x+3y=-(30)/(3)\\2x+3y=-10`