Question

Find the equation, in slope-intercept form, of the line through the pair of points

(1,-2) (-3,4)

Answer 1

`y=-(3)/(2)x+(7)/(2)`

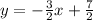
Explanation:

We do not have enough information for slope intercept form. But we can use the point-slope formula to find the information. The formula is
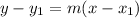`y -y_(1) =m(x -x_(1))` where we substitute a point (x,y) for
`(x_(1),y_(1))`.

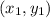We do not have m for the slope. But we do have (1,-2) and (-3, 4). We input the points for
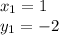`x_(1) =1\\y_(1)=-2` and
`x=-3\\y=4`.

`(4-(-2))=m (-3-1)`

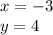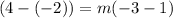
We now simplify the parenthesis and solve for m.

`(4+2)=m (-3+-1)\\6=m(-4)=`

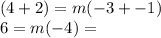
We divide by -4 on both sides and find
`m=-(6)/(4) =-(3)/(2)`. We substitute m into the point slope form with one coordinate pair.

`y-(-2)=-(3)/(2)(x-1)\\y+2=-(3)/(2)(x-1)\\y+2=-(3)/(2)x+(3)/(2)\\y+2-2=-(3)/(2)x+(3)/(2)-2\\y=-(3)/(2)x+(3)/(2)+(4)/(2) \\y=-(3)/(2)x+(7)/(2)`

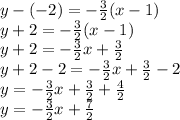
After simplifying the parenthesis, we subtracted 2 from both sides. We converted 2 into a fraction with 2 as the denominator.

This is slope intercept form
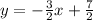`y=-(3)/(2)x+(7)/(2)`. The line has slope -3/2 and y-intercept (0,7/2) or b=7/2.