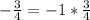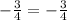Question

The equations of three lines are given below. Line 1: y = - 3/4 x + 3 Line 2/8 x - 6y = 2 Line 3/- 3y = 4x + 7 For each pair of lines, determine whether they are parallel, perpendicular, or neither.

Answer 1

No parallel lines

Lines 1 and 3 are perpendicular

Explanation:

Given:

`Line\ 1:y = -(3)/(4)x + 3`

`Line\ 2: (2)/(8)x -6y = 2`

`Line\ 3: 3y = 4x + 7`

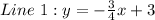
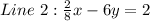
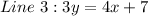
Required

Determine if they are parallel, perpendicular or not

The slope intercept of a line has the form:

`y = mx + b`

Where

`m = slope`

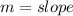
First, we calculate the slope of each lines

`Line\ 1:y = -(3)/(4)x + 3`

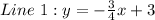
Compare the above to
`y = mx + b`

`m_1 = -(3)/(4)`

`Line\ 2: (2)/(8)x -6y = 2`

`(2)/(8)x -6y = 2`

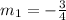
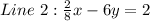
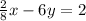
Make -6y the subject

`-6y = 2 - (2)/(8)x`

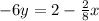
Divide through by -6

`y = -(2)/(6) + (2)/(8*6)x`

`y = -(1)/(3) + (1)/(8*3)x`

`y = -(1)/(3) + (1)/(24)x`

`y = (1)/(24)x-(1)/(3)`

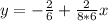
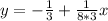
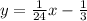
Compare the above to
`y = mx + b`

`m_2 = (1)/(24)`

`Line\ 3: 3y = 4x + 7`

`3y = 4x + 7`

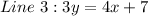
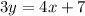
Divide through by 3

`y = (4)/(3)x + (7)/(3)`

Compare the above to
`y = mx + b`

`m_3 = (4)/(3)`

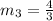
So, we have:

`m_1 = -(3)/(4)`

`m_2 = (1)/(24)`

`m_3 = (4)/(3)`

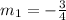
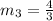
None of the slopes are the same, so none of the lines are parallel.

However, lines 1 and 3 are perpendicular.

This is shown below

When the slope of two lines satisfy the following condition, then they are perpendicular.

`m_1 = -(1)/(m_3)`

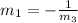
This gives:

`-(3)/(4) = -(1)/(4/3)`

`-(3)/(4) = -1/(4)/(3)`

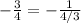
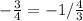
Convert / to *

`-(3)/(4) = -1*(3)/(4)`

`-(3)/(4) = -(3)/(4)`