Question

Which of the following is a valid exclusion for the algebraic fraction 8ab^2x/4a^2b-8ab^2

Answer 1

A valid exclusion for the algebraic fraction is when a=2b

Explanation:

You have:

`8ab^2x/4a^2b-8ab^2`

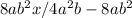
First you must to simplify:

Taking out common factor 4ab

`4ab(2bx)/4ab(a-2b)`

`2bx/a-2b`

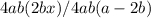
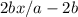
The fraction can be written only if the denominator is different to zero, then

a-2b
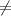`\\eq`0

the excluded values are where

a-2b=0

this expression is equal to 0 when a=2b

Answer 2

a ≠ 2b

Explanation:

The given expression is

`(8ab^(2)x)/(4a^(2)b-8ab^(2))`

`=(8ab^(2)x)/(4ab(a-2b))`

Simplifying it, we have

`(8ab^(2)x)/(4a^(2)b-8ab^(2)) = (bx)/(a-2b)`

For the above fraction to exist, the denominator must not be equal to zero.

i.e, a-2b ≠ 0

=> a≠2b

∴ The algebraic fraction exists when a≠2b.