Question

35 pts!! Please help this will help me graduate!!!

Consider this system of equations:

-3x + 5y = 22 (equation 1)
20y − 11 = 12x (equation 2)
This system of linear equations represents ___lines.
(A. coincidental B. Intersecting C. parallel)
The system of equation 1 and the equation 20y = 12x + 88 represents___ lines.
(A. coincidental B. Intersecting C. parallel)

Answer 1

This system of linear equations represents parallel lines.

The system of equation 1 and the equation 20y = 12x + 88 represents coincidental lines

Explanation:

-3x + 5y = 22 (equation 1)

Lets solve the equation for y

Add 3x on both sides

5y= 3x+22

Now divide by 5 on both sides

`y=(3x)/(5)+ (22)/(5)`

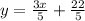
Slope of equation 1 is
`(3)/(5)`

20y − 11 = 12x (equation 2)

solve for y

Add 11 on both sides

20y = 12x + 11

Divide by 20 on both sides

`y=(12x)/(20)+ (11)/(20)`

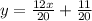
simplify the fraction

`y=(3x)/(5)+ (11)/(20)`

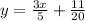
Slope of equation 2 is
`(3)/(5)`

Slope of equation 1 and equation 2 are same , so the lines are parallel

This system of linear equations represents parallel lines.

-3x + 5y = 22 (equation 1) and 20y = 12x + 88

Solve both equations for y

-3x + 5y = 22 (equation 1)

`y=(3x)/(5)+ (22)/(5)`

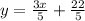
Slope of equation 1 is
`(3)/(5)` and y intercept is 22/5

20y = 12x + 88

Divide by 20 on both sides and simplify the fraction

`y=(3x)/(5)+ (22)/(5)`

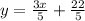
Slope of 20y=12x+88 is
`(3)/(5)` and y intercept is 22/5

Slope and y intercepts are same so the lines are coincidental

The system of equation 1 and the equation 20y = 12x + 88 represents coincidental lines