Question

El lunes joe compró 10 tazas de café y 5 donas para su oficina a un costo total de 16.50 el martes compró 5 tazas de café y 10 donas por un costo total de 14.25 ¿cuánto costaba cada taza de café?

Answer 1

Cada taza de café costaba 1.25

Explanation:

Un sistema de ecuaciones lineales es un conjunto de ecuaciones lineales que tienen más de una incógnita. Es decir, un sistema de ecuaciones es un conjunto de dos o más ecuaciones con varias incógnitas.

Resolver un sistema de ecuaciones consiste en encontrar el valor de cada incógnita para que se cumplan todas las ecuaciones del sistema.

En este caso, para definir el sistema de ecuaciones es necesario definir las variables:

• x: precio de una taza de café
• y: precio de una dona

Entonces si el lunes Joe compró 10 tazas de café y 5 donas para su oficina a un costo total de 16.50, se puede plantear la ecuación: 10*x +5*y=16.50

Si el martes Joe compró 5 tazas de café y 10 donas por un costo total de 14.25, podes plantear la ecuación: 5*x + 10*y=14.25

Entonces el sistema de ecuaciones a resolver es:

`\left \{ {{10*x+5*y=16.50} \atop {5*x+10*y=14.25}} \right.`

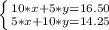
Se desea conocer el valor de cada taza de café, es decir, el valor de x. Para eso podes usar el método de sustitución, que consiste en despejar una de las incógnitas en una de las ecuaciones y sustituir su valor en la siguiente.

En este caso aislas el valor de y de la primer ecuación:

`y=(16.50-10*x)/(5)`

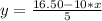
Reemplazando en la segunda ecuación:

`5*x+10*(16.50-10*x)/(5)=14.25`

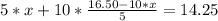
y resolviendo obtenes:

`5*x+(10)/(5)*(16.50-10*x)=14.25`

`5*x+2*(16.50-10*x)=14.25`

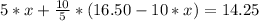
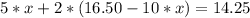
5*x + 2*16.50 -2*10*x=14.25

5*x + 33 - 20*x=14.25

5*x - 20*x=14.25 - 33

(-15)*x= -18.75

x= (-18.75)÷(-15)

x= 1.25

Entonces, cada taza de café costaba 1.25