Question

20 POINTS

Let f(x)=8(3)^x−2 +2 .


The graph of f(x) is stretched vertically by a factor of 3 to form the graph of g(x) .


What is the equation of g(x)


?




Enter your answer in the box.

Answer 1

`g(x)= 24(3)^(x-2)+6`

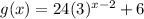
Explanation:

f(x)=8(3)^x−2 +2

The graph of f(x) is stretched vertically by a factor of 3 to form the graph of g(x)

When f(x) is stretched vertically then we multiply f(x) by 3 to get g(x)

g(x) = 3f(x)

`g(x)= 3(8(3)^(x-2)+2)`

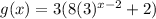
Now we distribute 3 inside the parenthesis

`g(x)= 24(3)^(x-2)+6`

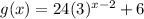
This is our required g(x)