For 1 and 2, you plot both lines, and wherever they intersect is the solution to the system. Given the equation of a line, I think the easiest way to plot it is to find two points on the line, then draw a line through them. For example, if
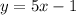 , then when
, then when
 , you get
, you get
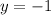 ; when
; when
 , you get
, you get
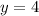 . So plot the points (0, -1) and (1, 4), then strike a line through.
. So plot the points (0, -1) and (1, 4), then strike a line through.
1. Notice that dividing both sides of
 by 2 returns
by 2 returns
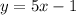 , same as the first equation. So the system of equations reduces to one equation, which can have an infinite number of solutions. (This is because for any choice of
, same as the first equation. So the system of equations reduces to one equation, which can have an infinite number of solutions. (This is because for any choice of
 or
or
 , you can always find a corresponding value for the other variable.)
, you can always find a corresponding value for the other variable.)
2. See attached image.
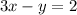 is given by the purple line.
is given by the purple line.
For 3-6, you have several options. The two simplest methods of solving them are by substitution or elimination.
3. Like with (1), notice that dividing both sides of the first equation by 2 gives
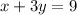 , so there will be an infinite number of solutions.
, so there will be an infinite number of solutions.
4. (by substitution) Since
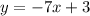 , we can replace
, we can replace
 in the second equation:
in the second equation:
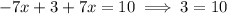
but this is false, so there are no solutions to this system.
5. (by substitution) Since
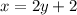 , in the first equation we have
, in the first equation we have
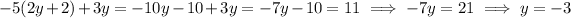
Then back in the second equation we find
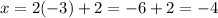
So (-4, -3) is the only solution here.
6. (by substitution) Notice that the left hand sides of both equations are the same, so we end up with 7 = 12, but this is false, so no solution exists.