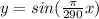Question

The graph of the sine curve below is of electromagnetic energy that represents green light:

sine graph with points at 0, 0 and 145, 1 and 290, 0 and 435, negative 1 and 580, 0

What function accurately represents the sine curve for green light?

Answer 1

what they said is correct

Step-by-step explanation

I took the test

Answer 2

y=sin((pi/290)x)

Explanation:

If we look at all the coordinates given (0,0),(145,1),(290,0),(435,-1),(580,0) we can draw it out and see what are our maximum and minimum y-value. Once you graph this you will notice that the maximum y-value is 1 and minimum y-value is -1, this is important because we call this our amplitude. Now we will determine our midline, we do so by getting the average of our amplitude so
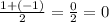`(1+(-1))/(2)=(0)/(2) =0` and so our midline is zero. Next we will determine our period in terms of radians we can do so by looking at our period which happens to be 580. This means that the line will repeat itself every 580 on the numberline and so:

`P=(2\pi )/(B)\\ \\580=(2\pi)/(B)\\\\B=(2\pi)/(580) \\\\B=(\pi)/(290)`

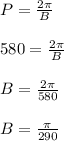
Therefore our period in radians is pi/290.

A sine function is such that:

`y=Asin(Bx)+D`

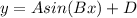
where A is the amplitude, B is the period, and D is the midline. Our amplitude is 1, midline is zero and our period is pi/290 and so our final equation is:

`y=sin((\pi)/(290)x)`