Question

Use row reduction to solve the system of equations.

Answer 1

`x=-1223,y=-629,z=-31`

Explanation:

The given systems of equations is

`x-2y+z=4`

`3x-5y-17z=3`

`2x-6y+43z=-5`

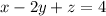
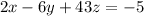
The augmented matrix is

`\left[\begin{array}{cccc}1&-2&1&|\:\:\:\:4\\3&-5&-17&|\:\:\:\:3\\2&-6&43&|-5\end{array}\right]`.

We perform the following row operations to reduce the matrix to reduced row echelon form using row 1 as our pivot row.

`R_2-3R_1\rightarrow R_2`

`R_3-2R_1\rightarrow R_3`

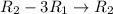
`\left[\begin{array}{cccc}1&-2&1&|\:\:\:\:\:\:\:\:\:\:4\\0&1&-20&|\:\:\:\:-9\\0&-2&41&|-13\end{array}\right]`

Next, we perform the following row operations using row 2 as our pivot row to obtain,

`R_1+2R_2\rightarrow R_1`

`R_3+2R_2\rightarrow R_3`

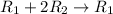
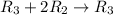
`\left[\begin{array}{cccc}1&0&-39&|-14\\0&1&-20&|\:\:-9\\0&0&1&|-31\end{array}\right]`

Next, we perform the following row operations using row 3 as our pivot row to get,

`R_1+39R_3\rightarrow R_1`

`R_2+20R_3\rightarrow R_2`

`\left[\begin{array}{cccc}1&0&0&|\:-1223\\0&1&0&|\:\:\:\:-629\\0&0&1&|\:\:\:\:\:\:-31\end{array}\right]`

The matrix is now in the reduced row echelon form,

Therefore the solution is,

`x=-1223,y=-629,z=-31`