Answer:
The length of the shorter part of the wire is 24 centimeters.
Explanation:
Let
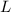 the total length of the piece of wire, where
the total length of the piece of wire, where
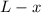 and
and
 are the perimeters of the greater and lesser squares. All lengths are measured in centimeters. Since squares have four sides of equal length, the side lengths for the greater and lesser squares are
are the perimeters of the greater and lesser squares. All lengths are measured in centimeters. Since squares have four sides of equal length, the side lengths for the greater and lesser squares are
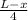 and
and
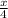 . From statement we find that the sum of the areas of the two squares (
. From statement we find that the sum of the areas of the two squares (
 ), measured in square centimeters, is represented by the following expression:
), measured in square centimeters, is represented by the following expression:
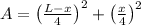 (1)
(1)
And we expand this polynomial below:
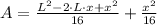

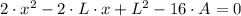 (2)
(2)
If we know that
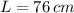 and
and
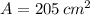 , then the length of the shorter part of the wire is:
, then the length of the shorter part of the wire is:
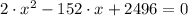
By the Quadratic Formula, we determine the roots associated with the polynomial:
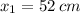 ,
,
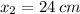
The length of the shorter part of the wire corresponds to the second root. Hence, the length of the shorter part of the wire is 24 centimeters.