Answer:
415.63 minutes
Explanation:
Growth can be represented by the equation
 . We can find the rate at which it grows by using t=25 minutes and
. We can find the rate at which it grows by using t=25 minutes and
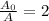 or double the amount at that time. The first step we always take is to divide
or double the amount at that time. The first step we always take is to divide
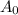 by A.
by A.
)/(A)=e^(rt)\\2=e^(r(25))](https://img.qammunity.org/2019/formulas/mathematics/high-school/dxczufq7c6zwxqte5uac70che8b75p0v5t.png)
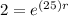
To solve for r, we will take the natural log of both sides and use log rules to isolate r.

We know
 so we were able to cancel it out and divide both sides by 25.
so we were able to cancel it out and divide both sides by 25.
We solve with a calculator
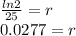
We change 0.0277 into a percent by multiplying by 100 to get 2.77% as the rate.
The equation is
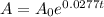 .
.
We repeat the step above substituting A=5,000,000,
 =50, and r=0.02777. Then solve for t.
=50, and r=0.02777. Then solve for t.
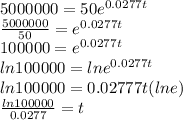
t=415.63 minutes