Answer:
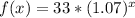
Explanation:
Let f(x) be our exponential growth function representing growth after x years.
We are asked to find the exponential function that satisfies the given conditions: Initial value = 33, increasing at a rate of 7% per year.
Since an exponential growth function is in form:
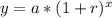 , where a= initial value of function and r = growth rate in decimal form.
, where a= initial value of function and r = growth rate in decimal form.
Given:
a=33
r=7%.
Let us convert our given rate in decimal form.

Now let us substitute our given values in exponential function form:

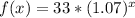
Therefore, the exponential function that satisfies our given conditions will be
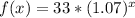 .
.