Question

A ladder that is 20 ft. Long is leaning against the side of a building. If the angle formed between the ladder and the ground is 75, how far is the bottom of the ladder from the base of the building?

Answer 1

The ladder from the base of the building is 5.18 ft (Approx)

Explanation:

As given

A ladder that is 20 ft. Long is leaning against the side of a building.

If the angle formed between the ladder and the ground is 75.

Now using the trignometric property .

`cos\theta = (Base)/(Hypotenuse)`

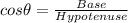
As shown in the figure.

`\theta = 75^(\circ)`

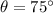
Base = CB

Hypotenuse = AC = 20 ft.

Put in the trignometric identity .

`cos75^(\circ) = (CB)/(AC)`

`cos75^(\circ) = (CB)/(20)`

`cos\ 75^(\circ) = 0.259`

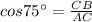
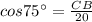
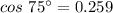
Put in the above

`0.259= (CB)/(20)`

`0.259 = (CB)/(20)`

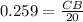
CB = 0.259 × 20

CB = 5.18 ft (Approx)

Therefore the ladder from the base of the building is 5.18 ft (Approx) .