NOTES:
Degree: the largest exponent in the polynomial
End Behavior:
- Coefficient is POSITIVE, then right side goes to POSITIVE infinity
- Coefficient is NEGATIVE, then right side goes to NEGATIVE infinity
- Degree is EVEN, then left side is SAME direction as right side
- Degree is ODD, then left side is OPPOSITE direction as right side
Multiplicity (M): the exponent of the zero. e.g. (x - 3)² has a multiplicity of 2
Relative max/min: the y-value of the vertices.
- Find the axis of symmetry (the midpoint of two neighboring zeros)
- Plug the x-value from 1 (above) into the given equation to find the y-value. (which is the max/min)
- Repeat 1 and 2 (above) for each pair of neighboring zeros.
Rate of Change: slope between the two given points.
********************************************************************************************
1. f(x) = (x-1)²(x + 6)
a) Degree = 3
b) end behavior:
- Coefficient is positive so right side goes to positive infinity
- Degree is odd so left side goes to negative infinity
c) (x - 1)²(x + 6) = 0
x - 1 = 0 x + 6 = 0
x = 1 (M=2) x = -6 (M=1)
d) The midpoint between 1 and -6 is -3.5, so axis of symmetry is at x = -3.5
y = (-3.5 - 1)²(-3.5 + 6)
= (-4.5)²(2.5)
= 50.625
50.625 is the relative max
e) see attachment #1
f) The interval at which the graph increases is: (-∞, -3.5)U(1, ∞)
g) The interval at which the graph decreases is: (-3.5, 1)
h) f(-1) = (-1 - 1)²(-1 + 6)
= (-2)²(5)
= 20
f(0) = (0 - 1)²(0 + 6)
= (-1)²(6)
= 6
Find the slope between (-1, 20) and (0, 6)
m =
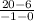
=
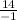
= -14
********************************************************************************************
2. y = x³+3x²-10x
= x(x² + 3x - 10)
= x(x + 5)(x - 2)
a) Degree = 3
b) end behavior:
Coefficient is positive so right side goes to positive infinity
Degree is odd so left side goes to negative infinity
c) x(x + 5)(x - 2) = 0
x = 0 x + 5 = 0 x - 2 = 0
x = 0 (M=1) x = -5 (M=1) x = 2 (M=1)
d) The midpoint between -5 and 0 is -2.5, so axis of symmetry is at x = -2.5
y = -2.5(-2.5 + 5)(-2.5 - 2)
= -2.5(2.5)(-4.5)
= 28.125
28.125 is the relative max
The midpoint between 0 and 2 is 1, so axis of symmetry is at x = 1
y = 1(1 + 5)(1 - 2)
= 1(6)(-1)
= -6
-6 is the relative min
e) see attachment #2
f) The interval at which the graph increases is: (-∞, -2.5)U(1, ∞)
g) The interval at which the graph decreases is: (-2.5, 1)
h) f(-1) = -1(-1 + 5)(-1 - 2)
********************************************************************************************
3. y = -x(x + 2)(x - 7)(x - 3)
a) Degree = 4
b) end behavior:
Coefficient is negative so right side goes to negative infinity
Degree is even so left side goes to negative infinity
c) -x(x + 2)(x - 7)(x - 3) = 0
-x = 0 x + 2 = 0 x - 7 = 0 x - 3 = 0
x = 0 (M=1) x = -2 (M=1) x = 7 (M=1) x = 3 (M=1)
d) The midpoint between -2 and 0 is -1, so axis of symmetry is at x = -1
y = -(-1)(-1 + 2)(-1 - 7)(-1 - 3)
= 1(1)(-8)(-4)
= 32
32 is a relative max
The midpoint between 0 and 3 is 1.5, so axis of symmetry is at x = 1.5
y = -(1.5)(1.5 + 2)(1.5 - 7)(1.5 - 3)
= -1.5(3.5)(-5.5)(-1.5)
= -43.3125
-43.3125 is the relative min
The midpoint between 3 and 7 is 5, so axis of symmetry is at x = 5
y = -(5)(5 + 2)(5 - 7)(5 - 3)
= -5(7)(-2)(2)
= 140
140 is the relative max
e) see attachment #3
f) The interval at which the graph increases is: (-∞, -1)U(1.5, 5)
g) The interval at which the graph decreases is: (-1, 1.5)U(5, ∞)
h) f(-1) = -(-1)(-1 + 2)(-1 - 7)(-1 - 3)
= 1(1)(-8)(-4)
= 32
f(0) = -(0)(0 + 2)(0 - 7)(0 - 3)
= 0
Find the slope between (-1, 32) and (0, 0)
m =
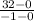
=
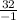
= -32