Question

If the 1kg standard body is accelerated by only f1=(3.O)+(4.0) and f2=(-2.0)+(-6.0) then what is fnet(al in unit vector notation and as (b) magnitude and (c) an angle relative to the positive x direction? What are the (d) magnitude and (e) angle of a ?

Answer 1

(a)
`\vec{F} = 1.0 \vec{i} - 2.0 \vec{j}`

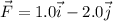
The two forces are:

`\vec{F_1} = 3.0 \vec{i} + 4.0 \vec{j}\\\vec{F_2} = -2.0 \vec{i} -6.0 \vec{j}`

To calculate the net force, we must calculate the resultant of the two vectors, which is obtained by separately summing the components of each vector:

`F_x = 3.0 \vec{i}+(-2.0) \vec{i} = 1.0 \vec{i}\\F_y = 4.0 \vec{j} + (-6.0) \vec{j} = -2.0 \vec{j}`

So, the net force is

`\vec{F} = 1.0 \vec{i} - 2.0 \vec{j}`

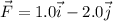
(b) 2.24 N

The magnitude of the net force is given by the Pythagorean theorem: it is equal to the square root of the sum of the squares of the single components:

`|F|= √(F_x^2+F_y^2)=√((1.0)^2+(-2.0)^2)=√(5)=2.24 N`

(c)
`-63.4^(\circ)`

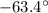
The angle of the net force, relative to the positive x direction, is equal to the arctangent of the ratio between the vertical component and the horizontal component:

`\theta=tan^(-1) ((F_y)/(F_x))=tan^(-1)((-2.0)/(1.0))=-63.4^(\circ)`

(d) 2.24 m/s^2

The mass of the object is m = 1 kg, so according to Newton's second law the acceleration is given by

`\vec{a} = \frac{\vec{F}}{m}`

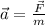
Since we are interested in the magnitude of the acceleration, we have to take the magnitude of the net force into the calculation:

`|a| = (|F|)/(m)=(2.23 N)/(1.0 kg)=2.24 m/s^2`

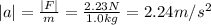
(e)
`-63.4^(\circ)`

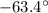
According to Newton's second law:

`\vec{a} = \frac{\vec{F}}{m}`

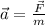
The acceleration has the same direction of the force, therefore the angle of the acceleration (measured with respect to the positive x direction) is
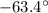`-63.4^(\circ)`.