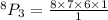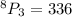Question

Evaluate 10c3 and 8p3

Answer 1

QUESTION 1

We want to evaluate

`^(10) C_3`

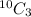
We use the formula,


`^(n) C_r = (n!)/(( n - r)!r!)`

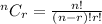
Substitute

`n = 10 \: and \: r = 3`
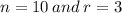
in to the above formula, to obtain,


`^(10) C_3= (10!)/(( 10 - 3)!3!)`


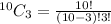
Simplify the right hand side to get,


`^(10) C_3= (10!)/(7!3!)`

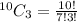
This implies that,



`^(10) C_3= (10 * 9 * 8 * 7!)/(7! * 3 * 2 * 1)`

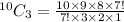
This simplifies to,


`^(10) C_3= (10 * 9 * 8)/(3 * 2 * 1)`


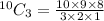
We cancel out common factors to get,


`^(10) C_3= (10 * 3 * 4)/(1 * 1* 1)`


`^(10) C_3= (120)/(1)`


`\therefore \: ^(10) C_3=120`


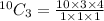
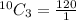
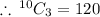
QUESTION 2


We want to evaluate

`^(8) P_3`

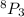
We apply the formula,


`^(n) P_r =(n!)/(( n - r)!)`


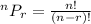
We substitute

`n = 8 \: and \: r = 3`
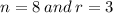
into the formula to get,.

`^(8) P_3=(8!)/(( 8 - 3)!)`


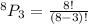
Simplify the right hand side to get,


`^(8) P_3=(8!)/(5!)`


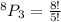
This will further give us,


`^(8) P_3=(8 * 7 * 6 * 5!)/(5!)`


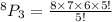
This will Simplify to,


`^(8) P_3=(8 * 7 * 6 * 1)/(1)`



`^(8) P_3=336`