Answer:
42 digits right of the decimal point.
Explanation:
Trailing zeroes are those which we get in decimal representation and after that there comes no digit.
We have been given the expression:
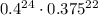
We will simplify it to get the result that is the right of the decimal point.
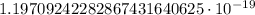
When we will operate
 that means decimal point will be shifted 19 digits left of its present position.
that means decimal point will be shifted 19 digits left of its present position.
Hence, we get:
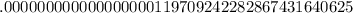
Hence, 42 digits right of the decimal point.