The division of

Let's divide the given polynomials:
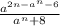
Divide the leading term of the numerator by the leading term of the denominator:
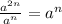 .
.
Multiply the entire denominator by the result from step 1 and subtract it from the numerator.
Bring down the next term and repeat steps 1 and 2 until you've gone through all the terms.
Here are the steps:
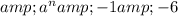
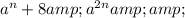
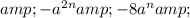
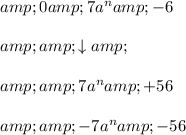
![& & 0 & 0\end{array} \]](https://img.qammunity.org/2019/formulas/mathematics/high-school/hduq1cduj1nqnpn0wyctn752wb7geg8pig.png)
The result is
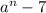 . Therefore, the division of
. Therefore, the division of
