Question

This upcoming week is finals week, and I need help lol

Answer 1

k=3

Explanation:

Given equation is

`x^2+y^2 -6y-12=0`

First we move -12 to the other side by adding 12 on both sides

`x^2+y^2 -6y =12`

We apply completing the square method to get square form (y-k)^2

Lets take coefficient of y and then divide it by 2

-6 divide by 2 is -3

Then we square it (-3)^2 = 9

We add 9 on both sides

`x^2+y^2 -6y + 9=12+9`

`x^2+(y^2 -6y + 9)=21`

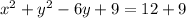
Now we factor, y^2 - 6y +9 is (y-3)(y-3)= (y-3)^2

`x^2+(y-3)^3=21`

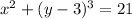
Now we compare with x^2 + (y-k)^2 = 21 and find the value of k

The value of k = 3