Question

David found and factored out the GCF of the polynomial 80b4 – 32b2c3 + 48b4c. His work is below.

GFC of 80, 32, and 48: 16
GCF of b4, b2, and b4: b2
GCF of c3 and c: c
GCF of the polynomial: 16b2c
Rewrite as a product of the GCF:
16b2c(5b2) – 16b2c(2c2) + 16b2c(3b2)
Factor out GCF: 16b2c(5b2 – 2c2 + 3b2)
Which statements are true about David’s work? Check all that apply.

The GCF of the coefficients is correct.
The GCF of the variable b should be b4 instead of b2.
The variable c is not common to all terms, so a power of c should not have been factored out.
The expression in step 5 is equivalent to the given polynomial.
In step 6, David applied the distributive property

Answer 1

The GCF of the coefficients is correct.

The variable c is not common to all terms, so a power of c should not have been factored out.

The expression in step 5 is equivalent to the given polynomial.

In step 6, David applied the distributive property

Explanation:

Only the above four statements are true.

GFC of 80, 32, and 48: 16

We find that 16 is the highest number which divides 80, 32 and 48. Hence 16 is GFC.

GCF of b4, b2, and b4: b2

Also we have taken the term of b in all three and found the least exponent as gCF hence correct.

Since c is not in the first term, no c term can be GCF hence iii is also true.

But the expression in step 5 is not equivalent to the given polynomial because I term in the step 5 =
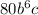`80b^6c`, but in the given no c term is there.

Yes. In step 6, he applied distributive property to take GCF outside the polynomial as a factor.

Answer 2

Given Polynomial:

`80b^4-32b^2c^3+48b^4c`

Factors of Coefficient of terms

80 = 5 × 16

32 = 2 × 16

48 = 3 × 16

Common factor of the coefficient of all term is 16.

Each term contain variable. So the Minimum power of b is common from all terms.

Common from all variable part comes b².

So, Common factor of the polynomial = 16b²

⇒ 16b² ( 5b² ) - 16b² ( 2c³ ) + 16b² ( 3b²c )

⇒ 16b² ( 5b² - 2c³ + 3b²c )

Therefore, Statements that are true about David's word are:

The GCF of the coefficients is correct.

The variable c is not common to all terms, so a power of c should not have been factored out.

In step 6, David applied the distributive property