Question

You have been tasked with filling 4 ounce and 3 ounce bags from a 41 ounce container of candy.

A. How many different combinations of full bags could you have?
B. If you would like to keep the total number of bags used to a minimum, which solution uses the fewest number of bags?
C. If 3 ounce bags cost 5 cents and 4 ounce bags cost 7 cents, which solution offers the cheapest way to fill the bags ?
D. If 3 ounce bags cost 5 cents and 4 ounce bags cost 6 cents, which solution offers the cheapest way to fill the bags ?
E. If the 4 ounce bags of candy sell for $2 each and the 3 ounce bags of candy sell for $1.50 each, which solution offers the greatest revenue?

Answer 1

A. 3 possible combinations

B. 8 4-ounce's bags and 3 3-ounce's bags

C. 2 4-ounce's bags and 11 3-ounce's bags

D. 8 4-ounce's bags and 3 3-ounce's bags

E. All solutions offer the same revenue.

Explanation:

You have been tasked with filling 4 ounce and 3 ounce bags from a 41 ounce container of candy. Let x be the number of 4 ounce bags and y be the number of 3 ounce bags. Then

`4x+3y=41.`

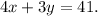
A. Find all integer solutions:

• When x=0, then 3y=41 - impossible, because 41 is not divisible by 3.

• When x=1, then 3y=37 - impossible, because 37 is not divisible by 3.

• When x=2, then 3y=33, y=11 - possible.

• When x=3, then 3y=29 - impossible, because 29 is not divisible by 3.

• When x=4, then 3y=25 - impossible, because 25 is not divisible by 3.

• When x=5, then 3y=21, y=7 - possible.

• When x=6, then 3y=17 - impossible, because 17 is not divisible by 3.

• When x=7, then 3y=13 - impossible, because 13 is not divisible by 3.

• When x=8, then 3y=9, y=3 - possible.

• When x=9, then 3y=5 - impossible, because 5 is not divisible by 3.

• When x=10, then 3y=1 - impossible, because 1 is not divisible by 3.

You get 3 possible combinations.

B. 1. 2 + 11 = 13,

2. 5 + 7 = 12,

3. 8 + 3 = 11.

The minimal number of bags is 11.

C. 1. 2·7+11·5=69 cents

2. 5·7+7·5=70 cents

3. 8·7+3·5=71 cents

The cheapest is 1st solution.

D. 1. 2·6+11·5=67 cents

2. 5·6+7·5=65 cents

3. 8·6+3·5=63 cents

The cheapest is 3rd solution.

E. 1. 2·2+11·1.50=$20.50

2. 5·2+7·1.50=$20.50

3. 8·2+3·1.50=$20.50

All solutions offer the same revenue.