Question

An astronaut on the moon throws a baseball upward. The astronaut is 6 ft, 6 in. tall, and the initial velocity of the ball is 40 ft per sec. The height s of the ball in feet is given by the equation s equals negative 2.7 t squared plus 40 t plus 6.5s=−2.7t2+40t+6.5 , where t is the number of seconds after the ball was thrown. Complete parts a and b. a. After how many seconds is the ball 12 ft above the moon's surface?

Answer 1

0.14 s

Explanation:

s = -2.7 t² + 40t + 6.5

Let s = 12

12 = -2.7t² + 40t + 6.5 Subtract 12 from each side

-2.7t² + 40t + 6.5 - 12 = 0

-2.7t² + 40t - 5.5 = 0

Apply the quadratic formula

`x = (-b\pm√(b^2-4ac))/(2a)`

a = -2.7; b = 40; c = -5.5

`x = \frac{-40\pm√(40^2 - 4* (-2.7) * (-5.5))} {2(-2.7)}`

`x = (-40\pm√(1600-59.4))/(-5.4)`

`x = (-40\pm√(1540.6))/(-5.4)`

`x = (-40\pm 39.25)/(-5.4)`

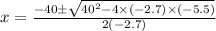
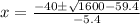
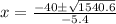
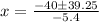
x = 7.41 ± 7.27

x₁ = 0.14; x₂ = 14.68

The graph below shows the roots at x₁ = 0.134 and x₂ = 14.68.

The Moon’s surface is at -12 ft. The ball will be 12 ft above the Moon’s surface (crossing the x-axis) in 0.14 s.

The second root gives the time the ball will be 12 ft above the Moon’s surface on its way back down.