Question

Two circular ponds at a botanical garden have the following radii. Pond A. 5√(164 ) meters

Pond B. (25√200)/5
Todd simplifies the radius of pond A this way: 5√(164 ) meters

Step 1: 5(√100+√64)
Step 2: 5(10+8)
Step 3: 5(18)
Step 4: 90
One of Todd’s steps is incorrect. Identify which step is incorrect; and rewrite the step so it is correct.

Answer 1

The correct step will be
`5(√(164))=5(√(4*41))`

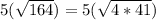
Explanation:

We have been given that pond A has a radius of
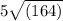`5√((164))` meters and radius of Pond B is
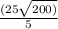`((25√(200)))/(5)` meters. Todd simplifies the radius of pond A and we are asked to find out error in Todd's steps.

Step 1:
`5(√(100)+√(64))`

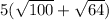
Since we know that
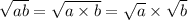`√(ab)=√(a* b)=√(a) * √(b)`. We can see that Todd has made error in his very first step by splitting
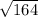`√(164)` as
`√(100+64)`.

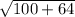The correct step will be,

`5(√(164))=5(√(4*41))`

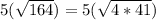
Therefore, the correct step 1 will be:
`5(√(4*41))`.

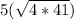Now let us simplify our given radical expression.

`5(√(4*41))=5(√(4)*√(41))`

`5√(4)*√(41)=5*2*√(41)`

`5*2*√(41)=10*√(41)`

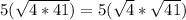
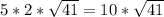
Therefore, our given radical expression simplifies to
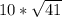`10*√(41)` meters.