Question

A 4​-ft vertical post casts a 14​-in shadow at the same time a nearby cell phone tower casts a 119​-ft shadow. How tall is the cell phone​ tower?

Answer 1

well if the shadow was 119 feet the tower would be 19 feet maybe? I think sorry if this is no help at all. But you could try it sorry again

Answer 2

The height of the cell phone tower is 408 feet.

Explanation:

This problem models a similarity between two right angles, one formed by the cell phone tower and its shadow, and the other formed by the vertical post and its shadow.

`h_(1)` is the height of the cell phone tower.

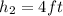`h_(2)=4ft` represents the height of the vertical post.

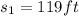`s_(1)=119ft` represents the shadow of the cell phone tower.

`s_(2)=14in=14in(1ft)/(12in)=(7)/(6) ft` represents the shadow of the vertical post.

Now, using the Thales theorem, we have

`(h_(1) )/(h_(2) ) =(s_(1) )/(s_(2) )\\ h_(1) =(s_(1) )/(s_(2) )h_(2)\\h_(1)=(119ft)/((7)/(6)ft) (4ft)\\h_(1)=(714)/(7)(4)=102(4)=408ft`

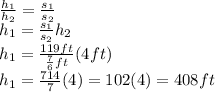
Therefore, the height of the cell phone tower is 408 feet.

Remember that Thales' theorem is about the proportions derived from to parallels and its intersection with two transversal. The important part of this theorem is to apply in the right order, that is, the ratio between height and the ratio between shadows, it would be wrong if we use a ratio between height and shadows, it can cause confusion.