Answer:
The area of ABCD is 36 cm².
Explanation:
Given information: ABCD is a parallelogram, E is the midpoint of BC and AE ∩ BD=F.
In triangle EBF and ADF
 (Alternate interior angles)
(Alternate interior angles)
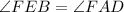 (Alternate interior angles)
(Alternate interior angles)
 (Vertically opposite angles)
(Vertically opposite angles)
Therefore triangle EBF and ADF are similar triangles by AA rule.
The sides BC and AD are opposite sides of parallelogram, therefore their lengths are equal. E is midpoint of BC.
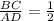
If a point divides the side of a triangle in m:n, then the line segment between the point and the opposite vertex, divides the area of triangle is m:n.
Therefore the sides of triangle are in proportion of 1:2 and we can say that the point F divides the line EA and BD in 1:2.
In triangle ABE, the line BF divides the area of triangle is 1:2.
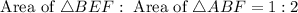
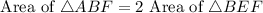

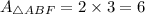
In triangle ABD, the line FA divides the area of triangle is 1:2.
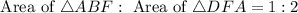
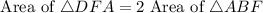

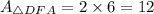
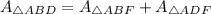
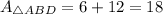
Since AD is a diagonal of the parallelogram, therefore AD divides the area of parallelogram in two equal parts.
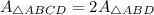
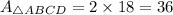
Therefore the area of ABCD is 36 cm².