Question

What are the vertical and horizontal asymptotes for the function fx=x^2+x-6/x^3-1?

A. vertical asymptote: x = 1 horizontal asymptote: none
B. vertical asymptote: x = 1 horizontal asymptote: y = 0
C. vertical asymptote: x = –2, x = 3 horizontal asymptote: y = 0
D. vertical asymptote: x = –2, x = –3 horizontal asymptote: none

Answer 1

Option B - Vertical asymptote: x = 1, horizontal asymptote: y = 0

Explanation:

Given : Function
`(x^2+x-6)/(x^3-1)`

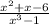
To find : What are the vertical and horizontal asymptotes for the function ?

Solution :

Function
`(x^2+x-6)/(x^3-1)`

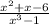
For vertical asymptote,

We equate the denominator to zero,

`x^3-1=0`

`\Rightarrow x^3=1`

`\Rightarrow x=1`

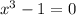
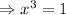
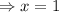
So, x=1 is the vertical asymptote.

For horizontal asymptote,

We compare the degree of numerator and denominator.

Degree of numerator is 2 and degree of denominator is 3.

When degree of denominator is greater than degree of numerator then y=0 is the horizontal asymptote.

So, y=0 is the horizontal asymptote.

Therefore, Option B is correct.