Question

if 2000 pounds is placed into a bank account that pays 3% compound interest per year, how much will be in the account after 2 years?

Answer 1

2121.8 pounds will be in the account after 2 years.

Step-by-step Step-by-step explanation:

Here's the required formula to find the Amount :

`\star{\small{\underline{\boxed{\sf{\purple{A = P\bigg(1 + (R)/(100)\bigg)^(T)}}}}}}`

• 
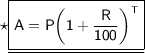
  `\pink\star` A = Amount
• 
  `\pink\star` P = Principle
• 
  `\pink\star` R = Rate
• 
  `\pink\star` T = Time

Substituting all the given values in the formula to find the Amount :

`\implies{\small{\sf{Amount = P \bigg(1 + (R)/(100) \bigg)^(T)}}}`

`\implies{\small{\sf{Amount = 2000 \bigg(1 + (3)/(100) \bigg)^(2)}}}`

`{\implies{\small{\sf{Amount = 2000 \bigg( (100 + 3)/(100) \bigg)^(2)}}}}`

`{\implies{\small{\sf{Amount = 2000 \bigg( (103)/(100) \bigg)^(2)}}}}`

`{\implies{\small{\sf{Amount = 2000 \bigg( (103)/(100) * (103)/(100)\bigg)}}}}`

`{\implies{\small{\sf{Amount = 2000 \bigg( (103 * 103)/(100 * 100)\bigg)}}}}`

`{\implies{\small{\sf{Amount = 2000 \bigg( (10609)/(10000)\bigg)}}}}`

`{\implies{\small{\sf{Amount = 2000 * (10609)/(10000)}}}}`

`{\implies{\small{\sf{Amount = 2000 * 1.0609}}}}`

`{\implies{\small{\sf{\underline{\underline{\red{Amount = 2121.8}}}}}}}`

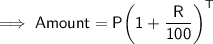
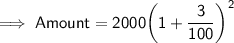
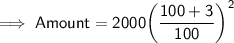
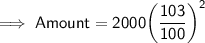
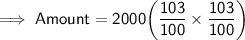
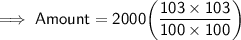
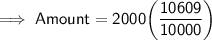
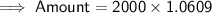
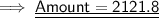
Hence, the amount is 2121.8 pounds.

`\rule{300}{2.5}`