Question

In a trapezoid the lengths of bases are 11 and 18. The lengths of legs are 3 and 7. The extensions of the legs meet at some point. Find the length of segments between this point and the vertices of the greater base.

Answer 1

Answer:
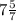`7(5)/(7)` unit and 18 unit

Step-by-step explanation:

Let ABCD is a trapezoid where AB and CD are the bases. ( In which AB is greatest base which shown in below figure)

AD and BC are the legs of the trapezoid ABCD.

Now, we have ( According to the question ),

AB = 18 unit, BC = 7 unit, AD = 3 unit and DC = 11 unit.

Here the leg AD extends from point D.

Similarly leg BC extends from point C.

Let they meet at point P ( shown in below diagram)

Since In triangles PAB and PDC,

∠PDC ≅ ∠PAB ( because DC ║ AB )

And, ∠ PAB ≅ ∠ PBA

∠DPC ≅ ∠ APB ( reflexive)

Therefore, By AAA similarity postulate,

`\triangle PDC \sim \triangle PAB`

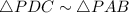
Thus, By the definition of similarity,

`(PD)/(PA) = (DC)/(AB)`

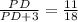`(PD)/(PD+3) = (11)/(18)` ( because PA = PD+DA)

⇒ 18 PD = 11 PD +33

⇒7PD = 33

⇒ PD = 33/7

Again by the definition of similarity,

`(PC)/(PB) = (DC)/(AB)`

`(PC)/(PC+7) = (11)/(18)` ( because PB = PC + CB)

⇒ 18 PC = 11 PD +77

⇒7PC = 77

⇒ PC = 11

Thus, PA = PD+DA = 33/7 + 3 =
`7(5)/(7)`

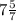
And, PB = PC + CB = 11 + 7 = 18