Answer:
3.7 km/h
Step-by-step explanation:
Let's call v the proper speed of the boat and v' the speed of the water in the river.
When the boat travels in the direction of the current, the speed of the boat is:
v + v'
And it covers 50 km in 3 h, so we can write
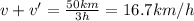 (1)
(1)
When the boat travels in the opposite direction, the speed of the boat is
v - v'
And it covers 50 km in 5.4 h, so
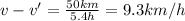 (2)
(2)
So we have a system of two equations: by solving them simultaneously, we find the value of v and v':
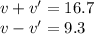
Subtracting the second equation from the first one we get:
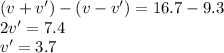
So, the speed of the water is 3.7 km/h.