Question

he law of cosines for RST can be set up as 52 = 72 + 32 – 2(7)(3)cos(S). What could be true about RST? Law of cosines: a2 = b2 + c2 – 2bccos(A)

Answer 1

answer is d on edge

Explanation:

Answer 2

The length of RT is 5. The length of RS and ST is either 7 or 3.

Explanation:

The Law of Cosine is defined as

`a^2=b^2+c^2-2bc\cos(A)`

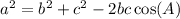
It is given that, the law of cosine for triangle RST can be set up as

`5^2=7^2+3^2-2(7)(3)\cos(S)`

Therefore the length of opposite side of angle S is 5. The opposite side of angle S is RT, therefore the length of RT is 5.

The length of two other sides are either 7 or 3.

Therefore length of RT is 5. The length of RS and ST is either 7 or 3.