Answer:
The area of the rectangle is 9.
Explanation:
The first thing to take into account is that the area of a rectangle is obtained by multiplying its length and width.
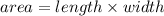
The problem says that the length is
![\sqrt[3]{81}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/s6itvkx9u4fivkogcme6pocp7o27v31yid.png) and the width is
and the width is
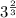 . So, to find the area we must replace the values of length and width into the previous expression.
. So, to find the area we must replace the values of length and width into the previous expression.
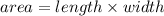
![area=(\sqrt[3]{81})* (3^{(2)/(3)})](https://img.qammunity.org/2019/formulas/mathematics/middle-school/rcvnahpzmgy7i530yzoy49jiqcafz50t9u.png)
The previous seems to be difficult but with a little of manipulation we can get a result without a calculator.
First step: the term
![\sqrt[3]{81}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/s6itvkx9u4fivkogcme6pocp7o27v31yid.png) could be written as exponential expression.
could be written as exponential expression.

Second step: the term
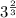 could be written in other way.
could be written in other way.

Third step: in the same way, the term
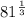 could be written in other way taking into account that
could be written in other way taking into account that
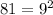 .
.
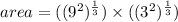
Forth step: the two terms must have the same base to apply other exponential rules; for example, the base could be 9.
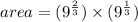
Fifth step: as both terms have the same base, we must add the exponents and simplify the expression.
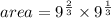
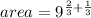
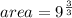
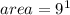
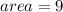
Thus, the area of the rectangle is 9.