Answer:
9.91 miles
Explanation:
Refer the attached figure
Forest Ranger at point A observes the fire at angle of 41° north of east i.e.∠CAB = 41°
The distance between the two rangers is 15 miles i.e. AB = 15 miles
Forest Ranger at point B observes the fire at at 56° north of west. i.e.∠CBA= 56°
Now we are supposed to find who is closest to the fire
So, we are supposed to find the length of AC and BC
So, first calculate ∠ACB
We will use angle sum property of triangle
Angle sum property of triangle : Sum of all angles of triangle is 180°
So, ∠CBA+∠ACB+∠CAB =180°
56°+∠ACB+41° =180°
97°+∠ACB =180°
∠ACB =180°-97°
∠ACB =83°
Now to find AC and BC we will use law of sines
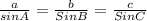
Refer the attached figure
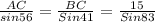
So,

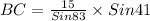
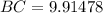
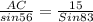
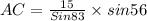
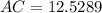
So, BC< AC
So, the ranger who is closest to fire is at a distance of 9.91 miles .
So, Option 1 is true