Answer:
306
Explanation:
We know that the formula of an arithmetic sequence with the same common difference is given by:
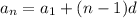
where
 is the term that we want to find out,
is the term that we want to find out,
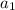 is the first term of the sequence,
is the first term of the sequence,
 is the number or position of the unknown term; and
is the number or position of the unknown term; and
 is the common difference.
is the common difference.
Here,
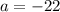 and
and
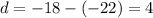 .
.
So putting in these values in the formula to get:

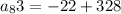
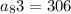
Therefore, the 83rd term of the given sequence is 306.