Question

The length of the base and the height of a triangle are numerically equal. Their sum is 30 less than the number of units in the area of the triangle. Find the area of the triangle.

Answer 1

50 sq. units

Explanation:

The length of the base and the height of a triangle are numerically equal.

Let us assume that, the length and height as x.

So the area of the triangle will be,

`\text{Area}=(1)/(2)\cdot \text{Base}\cdot \text{Height}=(x^2)/(2)`

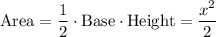
As their sum is 30 less than the number of units in the area of the triangle, so

`\Rightarrow x+x=(x^2)/(2)-30`

`\Rightarrow 2x=(x^2)/(2)-30`

`\Rightarrow 4x=x^2-60`

`\Rightarrow x^2-4x-60=0`

`\Rightarrow x^2-10x+6x-60=0`

`\Rightarrow x(x-10)+6(x-10)=0`

`\Rightarrow (x+6)(x-10)=0`

`\Rightarrow (x+6)=0,(x-10)=0`

`\Rightarrow x=-6,x=10`

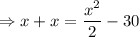
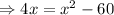
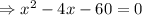
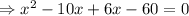
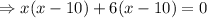
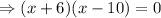
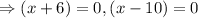
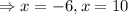
Neglecting negative roots,

`\Rightarrow x=10`

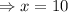
Hence, the base and height of the triangle is 10 units, so the area will be,

`\text{Area}=(1)/(2)\cdot \text{Base}\cdot \text{Height}=(1)/(2)\cdot 10\cdot 10=50\ unit^2`