Answer:
617.5
Explanation:
If you expand the series by putting in
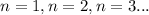 values, you will see:
values, you will see:
- Put 1 in
 ,
,
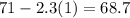
- Put 2 in
 ,
,
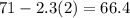
- Put 3 in
 ,
,
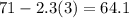
68.7, 66.4, 64.1, ....
To find common difference (d) (difference in a term and its previous term) we take any term and subtract from it the term before it:
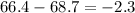
The sum of arithmetic series formula is:
![S_(n)=(n)/(2)[2a+(n-1)d]](https://img.qammunity.org/2019/formulas/mathematics/high-school/c42k3dlpg1peo6ex0ugqha2ythwfked3ew.png)
Where,
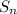 is the sum of nth term
is the sum of nth term- a is the first term (in our case it is 68.7)
- n is the term number (in our case we want to find 50th sum, so n = 50)
- d is the common difference (in our case it is -2.3)
Substituting these values, we get:
![S_(50)=(50)/(2)[2(68.7)+(50-1)(-2.3)]\\S_(50)=25[137.4+(49)(-2.3)]\\S_(50)=25[24.7]\\S_(50)=617.5](https://img.qammunity.org/2019/formulas/mathematics/high-school/pe1d6ija28nxv75xli7zu2469tccr6cntn.png)
Last answer choice is right.