Question

A standardized test was given to a set of high school juniors and the distribution of the data is bell shaped. The mean score is 800 and the standard deviation is 120.

To qualify for a special summer camp for accelerated students, a student must score within the top 16% of all scores on the test. What score must a student make to qualify for summer camp?

Answer 1

920 points.

Step-by-step explanation:

We have been given that the mean score for a standardized test is 800 and the standard deviation is 120. To qualify for a special summer camp for accelerated students, a student must score within the top 16% of all scores on the test.

First of all we will find probability of 0.16 using normal distribution table.

Using normal distribution our Z score will be 0.994458

Now we will use raw-score formula to find the score (x) that a student must make to qualify for summer camp.

`x=\text{Mean}+\text{ Standard deviation* Z score}`

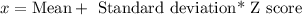
Upon substituting our given values in above formula we will get,

`x=800+120* 0.994458`

`x=800+119.33496`

`x=919.33496`

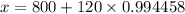
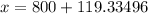
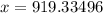
Upon rounding to nearest whole number we will get,

`x=920`

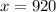
Therefore, a student must make 920 points to qualify for summer camp.