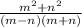Question

Express as one fraction: (m/m−n)−(n/m+n)

Answer 1

`(m^2+n^2)/((m-n)(m+n))`

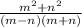
Explanation:

Before we can subtract the fractions we require them to have a common denominator.

the common denominator is (m - n)(m + n)

multiply the numerator/denominator of the first fraction by (m + n) and

multiply the numerator/denominator of the second fraction by (m - n)

=
`(m(m+n))/((m-n)(m+n))` -
`(n(m-n))/((m-n)(m+n))`

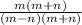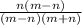
distribute and simplify the numerators

=
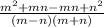
`(m^2+mn-mn+n^2)/((m-n)(m+n))`

=
`(m^2+n^2)/((m-n)(m+n))`

Answer 2

Answer: (m - 2mn - n)/m

Explanation:

(m/m-n) - (n/m+n)

[(m/m) - (mn/m)] - [(n/m) + (mn/m)]

[(m - mn)/m] - [(n+mn)/m]

(m - mn - n - mn) / m

(m - 2mn - n) / m