Question

Click an item in the list or group of pictures at the bottom of the problem and, holding the button down, drag it into the correct position in the answer box. Release your mouse button when the item is place. If you change your mind, drag the item to the trashcan. Click the trashcan to clear all your answers.

T.A. =

Answer 1

`T.A. = 18 + (9)/(4)√(3)`

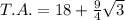
Explanation:

The figure can be decomposed in an equilateral triangle, with sides = 3'', and a rectangle with sides 3'' and 6''.

The area of an equilateral triangle (A1) is calculated as follows:

`A1 = (a^2 √(3))/(4)`

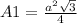
where a refers to the length of each side of the triangle. Here a = 3. Replacing:

`A1 = (3^2 √(3))/(4)`

`A1 = (9)/(4)√(3)`

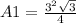
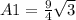
The area of the rectangle is: 3*6 = 18'' = A2

The total area (T.A) is the addition of A1 to A2, So:

`T.A. = 18 + (9)/(4)√(3)`

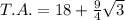
Notice that the line after after the + sign is not a subtract symbol, it is the line between numerator and denominator of the answer

Answer 2

The base is an equilateral triangle. The formula of the area of that triangle is:

`A=(a^2\sqrt3)/(4)`

a - length of side

a = 3". Substitute:

`A_B=(3^2\sqrt3)/(4)=(9\sqrt3)/(4)`

The lateral side is a rectangle.

`A_(LS)=3\cdot6=18`

The Total Area is equal the sum of two times of Base and three times of Lateral Side.

`T.A.=2\cdot(9\sqrt3)/(4)+3\cdot18=(9\sqrt3)/(2)+54\\\\\boxed{Answer:\ T.A.=54+4.5\sqrt3}`