Question

What is the monomial if a square of a monomial is: 1/4 a2n

Answer 1

`(1)/(2)a^n`

Explanation:

Givens:

• Square of a monomial:
  `(1)/(4) a^(2n)`.

The problem is asking for the monomial, and the given is squared. What we have to do is to extract that square from expression, and that it's done applying a squared root, because that's the opposite operation of a squared power:

`\sqrt{(1)/(4) a^(2n)}`

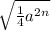
So, here we have to find the squared root of
`(1)/(4)` and
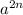`a^(2n)`, applying the root to each factor:

`\sqrt{(1)/(4)} \sqrt{a^(2n)}`

So, we know that a root can be expressed as a fractional exponent, and also the root of a fraction is the root of each part of the fraction:

`(√(1))/(√(4)) (a^(2n))^{(1)/(2) }`

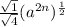
Now, we solve:

`(1)/(2)a^{(2n)/(2)}= (1)/(2)a^n`

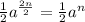
Therefore, the monomial expression is
`(1)/(2)a^n`

Answer 2

`(1)/(2) a^n`

Explanation:

Square of the monomial is
`(1)/(4)a^(2n)`

To get the monomial we take square root

Lets take square root for each term

`\sqrt{(1)/(4)a^(2n)}`

`\sqrt{(1)/(4)}=\fract{1}{2}` because square root of 4 is 2

`\sqrt{a^(2n)}=(a^(2n))^(1)/(2)`

2/2 is 1 so, its a^n

Required monomial is
`(1)/(2) a^n`