Question

In ΔABC, m∠A = 40°, m∠B = 60°. Find m∠C. (Hint: Draw the auxiliary line BD parallel to the line segment AC and take a look at the same side and the alternate interior angles)

Answer 1

The measure of angle C is 80 degree.

Explanation:

Given information: In ΔABC, ∠A = 40° and ∠B = 60°.

Draw the auxiliary line BD parallel to the line segment AC.

If a transversal line intersects the pair of parallel line, then the alternate interior angles are same.

The angle 1 and 2 are alternate interior angles of angle A and B respectively. Therefore angle 1 is equal to angle A and angle 2 is equal to angle C.

Angle 1,2 and B are supplementary angles because they lie on a straight line, therefore their sum is 180 degree.

`\angle 1+\angle B+\angle 3=180^(\circ)`

`\angle A+\angle B+\angle =180^(\circ)`

`40^(\circ)+60^(\circ)+\angle C=180^(\circ)`

`\angle C=180^(\circ)-100^(\circ)`

`\angle C=80^(\circ)`

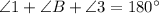
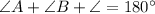
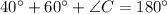
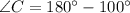
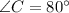
The angle sum property is another way to solve this problem.

According to the angle sum property, the sum of interior angles of a triangle is 180 degree.

Therefore the measure of angle C is 80 degree.