Question

How many integers $n$ satisfy the inequality 3n^2-4 <= 44

Answer 1

9

Explanation:

Answer 2

9 integers.

Step-by-step explanation:

We have been given an inequality
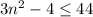`3n^2-4\leq 44` and we are asked to find the solution set for our given inequality.

Let us solve our given inequality by adding 4 to both sides of our equation.

`3n^2-4+4\leq 44+4`

`3n^2\leq 48`

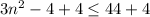
Upon dividing both sides of our equation by 3, we will get,

`(3n^2)/(3)=(48)/(3)`

`n^2\leq 16`

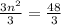
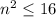
Taking square root of both sides of our equation we will get,

`n\leq \pm 4`

`-4\leq n\leq 4`

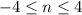
The solution set for our inequality is integers between -4 to 4 including -4 and 4 as : -4,-3,-2,-1,0,1,2,3,4.

Therefore, 9 integers will satisfy our given inequality.