Question

A cargo train and a passenger train, which start from two stations that are 710 km apart, are traveling towards each other. The cargo train started an hour before the passenger train, and is traveling with a speed of 110 km/hour. In how many hours will the cargo train and the passenger train meet, if the passenger train is traveling at 90 km/hour?

Answer 1

4 hours because the person asking the question didn’t include the actual question which is “The trains will meet in __ hours after departure of the the cargo train”

Explanation:

The other guy explained the “Almost answer”, but its the person who asked the questions fault. He got 3 hours but in the information part it says that the cargo train left a hour earlier sa you add one hour the 3 hours. So the answer is 4.

Answer 2

The trains will meet in 3 hours.

Explanation:

The initial distance between the trains was 710 km, but since the cargo train started an hour before the passenger train, it has already covered some distance towards it. The distance the cargo train has covered is simply the product of its speed
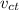`v_(ct)` and the time taken
`t`:

`D =v_(ct)t=(110km/hr)* 1hr =110km.`

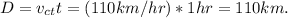
So the distance left between the trains is the starting distance minus this distance:

`D_(left)=710km-110km=600km.`

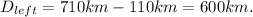
Now both trains are travelling towards each other, this means the rate at which the distance that is being covered is equal to the sum of the speeds of the trains:

`v_(tot)=v_(ct)+v_(pt)=(110km/hr)+(90km/hr)=200km/hr`

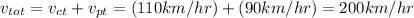
Now that we have the speed, it is easy to calculate the amount of time it will take for the trains to meet:

`t=(D_(left))/(v_(tot)) =(600km)/(200km/hr) =\boxed{3\:hours.}`

Thus the cargo train and the passenger train will meet in 3 hours.